Ocean Image Formation

The problem of light transport on land is relatively simple and well-modeled. However, the same cannot be said for the ocean, a complex medium with a variety of factors that affect light transport such as absorption and scattering of light by water, the reflection of light off the ocean surface, the influence of waves on the process, to name a few. In this post, we will explore how light transport in the ocean can be modeled and how this can be used to generate realistic ariel images of objects in the ocean with the ultimate goal of recovering a view of the object without the ocean.

I included a juypter notebook here that can be run as you read along here, from which you can find implementations for the methods described below.

Wave Formation

We first describe how waves are formed in the ocean. Specifically, consider a \(L_x\) by \(L_z\) (m) size patch modeled by a grid at resoluion \(N\) x \(M\). Each entry in the grid contains at time \(t\) a ocean surface height value \(h(x, z, t)\), a unit normal \(n(x, z, t)\), and a position \(r(x, z, t)\). The movie Titanic employed the Fast Fourier Transform (FFT) method to generate waves described in [1]. Specifically the ocean surface height \(h(x, z, t)\) is modeled as a sum of sinusoids with random phases and amplitudes.

First let’s consider our patch has size \(N\) and \(M\) at the same resolution. We can write the heightmap as

\[h(x, z, t) = \sum_{n=0}^{N-1}\sum_{m=0}^{M-1} \tilde{h}(n, m, t) e^{2\pi i\left(\frac{nx}{N} + \frac{mz}{M}\right)}\]

where \(\tilde{h}(n, m, t)\) is the Fourier amplitude of the wave at frequency \(m, n\). We will discuss how to obtain the Fourier amplitude later. We can scale the Fourier transform to any size \(L_x\), \(L_z\) using the scaling property, where \(f\) denotes the Euclidean domain and \(F\) frequency domain and \(a, b\) are the scaling factors

\[f(ax, by) = \frac{1}{|ab|}F\left(\frac{u}{a}, \frac{v}{b}\right)\]

from which we get

\[h(x, z, t) = S \sum_{n=0}^{N-1}\sum_{m=0}^{M-1} \tilde{h}(n, m, t) e^{2\pi i\left(\frac{nx}{L_x} + \frac{mz}{L_z}\right)}\]

where \(S = (NM)/(L_xL_z)\). The position can be expressed as

\[r(x, z, t) = \left( x, h(x, z, t), z\right)\]

The slope is given by the gradient of the height field, which can also be computed via FFT

\[\begin{align*} e(x, z, t) &=S \ \nabla h(x, z, t) =S\sum_{n=0}^{N-1}\sum_{m=0}^{M-1} 2\pi i \begin{bmatrix} n / L_x \\ m / L_z \end{bmatrix} \tilde{h}(n, m, t) e^{2\pi i\left(\frac{nx}{L_x} + \frac{mz}{L_z}\right)} \end{align*}\]

Let \(\hat{y}\) be the unit up vector. The normal is given by

\[n(x, z, t) = \hat{y} - \frac{e(x, z, t)}{\sqrt{1 + \|e(x, z, t)\|^2}}\]

Statisitcal analysis of waves have shown the Fourier amplitudes h(k, t) can be modeled by gaussian random variables according to the wave spectrum \(P_h(m, n)\) at time 0 as

\[\tilde{h}_0(m, n) = \sqrt{\frac{P_h(k)}{2}}(\mathcal{E}_1 + i\mathcal{E}_2)\]

where \(\mathcal{E}_1, \mathcal{E}_2\) are independent gaussians with zero mean and unit variance. Note since \(h\) is real, \(\tilde{h}(n, m, t) = \tilde{h}(N-n, M-m, t)\). Let \(w\) denote the wind vector. We specifically use the Phillips Spectrum, though other spectra can be used. The Phillips spectrum is given by

\[P_h(m, n) = \frac{A\exp\left(-1 / (kL)^2\right)}{k^4}\cos(\theta_{w})^p\]

where \(A\) is the Phillips constant, \(k = 2\pi\sqrt{(n / Lx)^2 + (m / L_z)^2}\) the wave vector, \(L = \frac{\|w\|^2}{g}\), \(g\) is gravity, \(\theta_{w}\) is the angle between the wind vector and the wave vector, and \(p\) controls the alignment between the wind and wave vectors e.g. 2 or 6. . This model has poor convergence properties at high values of the wavenumber \(k\). A simple fix is to suppress waves smaller that a small length \(\mathcal{l} < L\), and modify the Phillips spectrum by a damping factor \(\exp\left(-k^2\mathcal{l}^2\right)\).

Given a dispersion relation \(\omega(m, n)\), which describes how to wave at frequency \(m, n\) evolves over time, we can write

\[\tilde{h}(m, n, t) = \tilde{h}_0(m, n)e^{i\omega(m, n)t}\]

Note if we use \(\texttt{torch.fft.irfft2}\), the conjugation property is preserved as the negative frequencies of the last dimension are ignored. The dispersion relation is given by

\[\omega^2(m, n) = gk\tanh(kD)\]

for water of depth \(D\). For deep water, we can simplfy the expression as

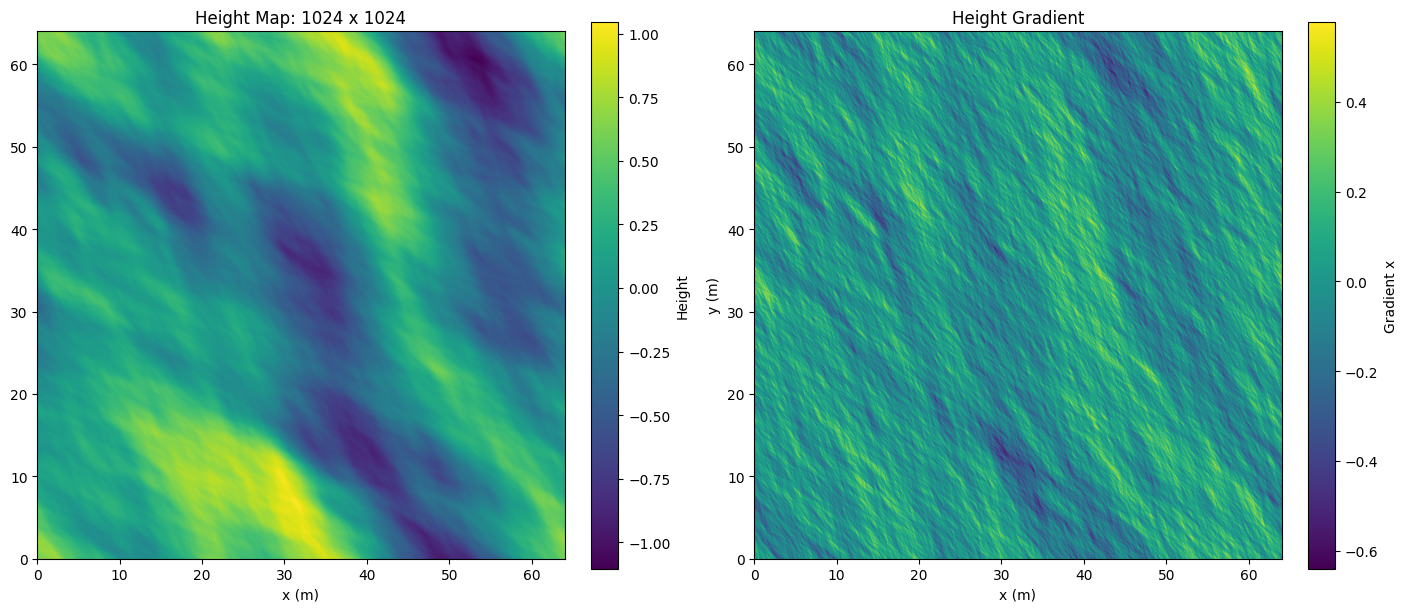
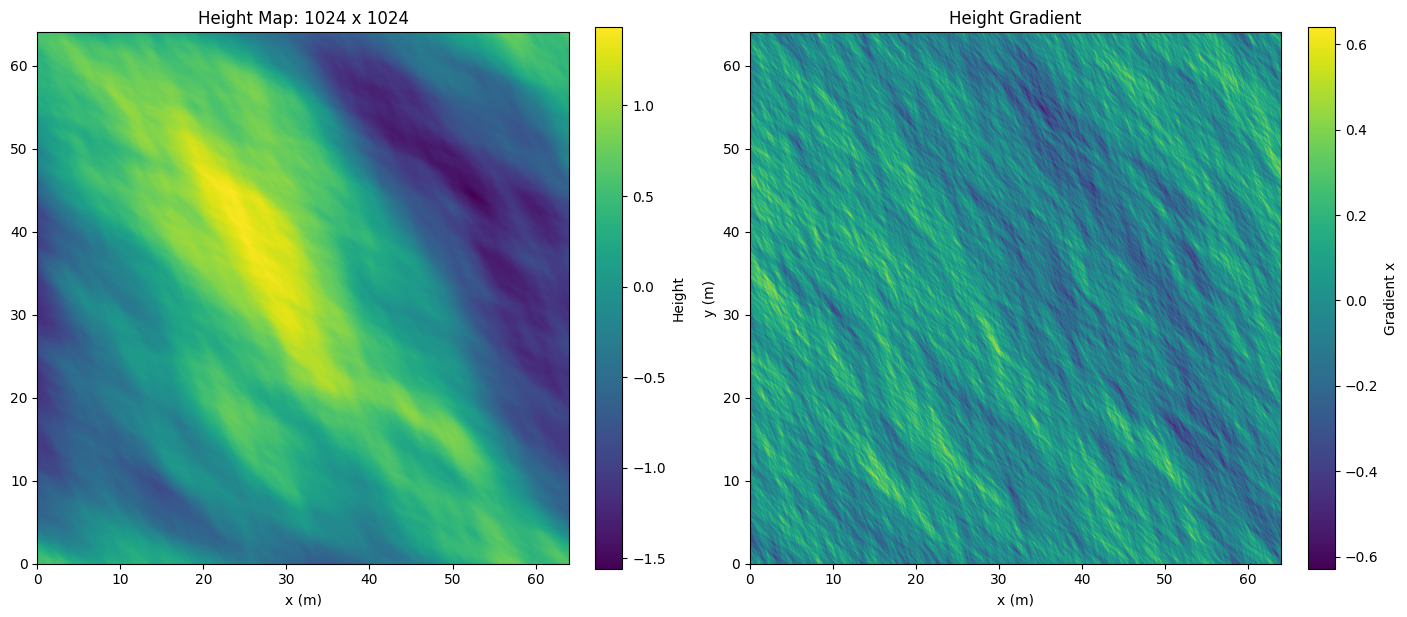
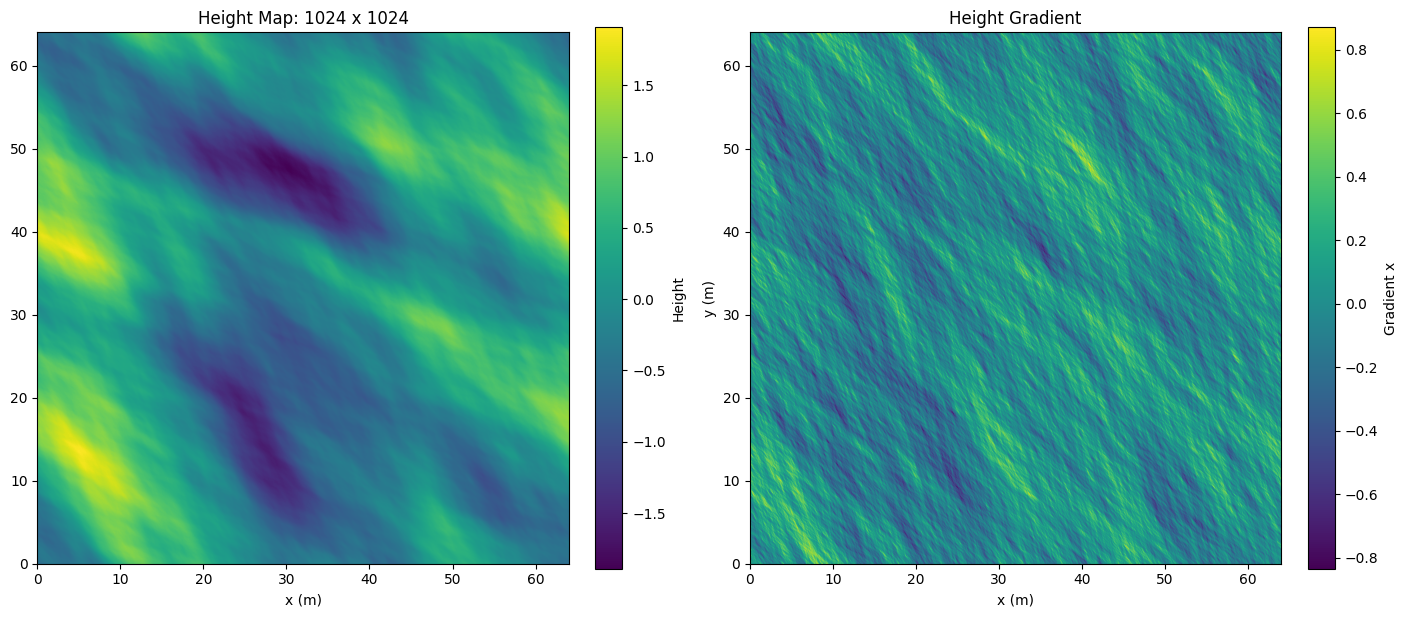
\[\omega^2(m, n) = gk\]

We show some examples of wave height and normal maps at different resolutions.

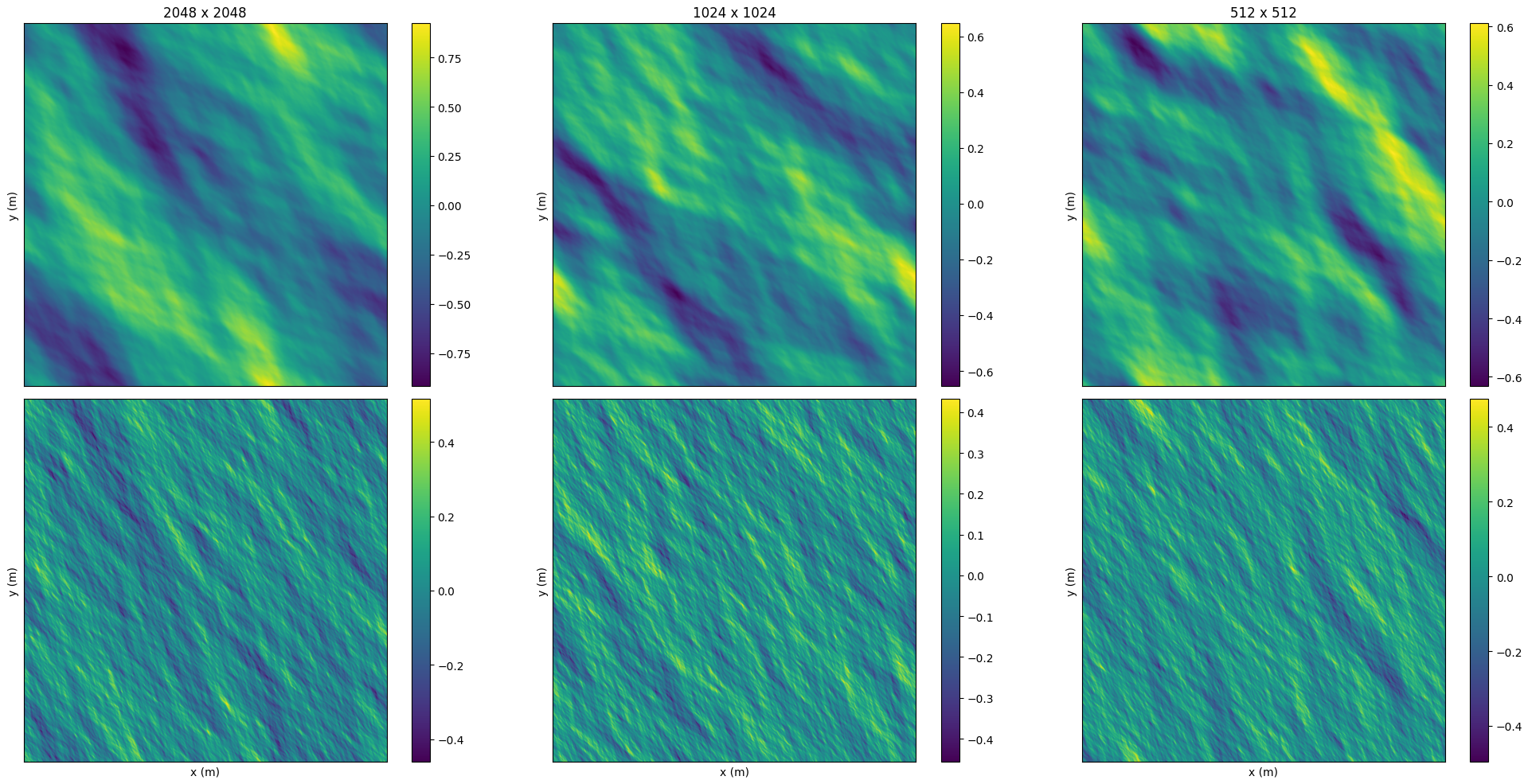
Parameter Choices

To quote directly from [1], the values of N and M can be between 16 and 2048, in powers of two. For many situations, values in the range 128 to 512 are sufficient. For detailed surfaces, 1024 and 2048 can be used. For example, the wave fields used in the motion pictures Waterworld and Titanic were 2048 × 2048 in size, with the spacing between grid points at about 3 cm. Above a value of 2048, one should be careful because the limits of numerical accuracy for floating point calculations can become noticeable. Since the wave behvaior below 1cm is not well modeled, \(\mathcal{l}\) can be set to something around that value.

Below is an example of a wave map generated at 1024 x 1024 resolution of a 64 x 64m patch of ocean. We set the Phillips constant to \(A=256\), use an alignment of \(\cos^6\), and supress waves smaller than \(10^{-3}\)cm.

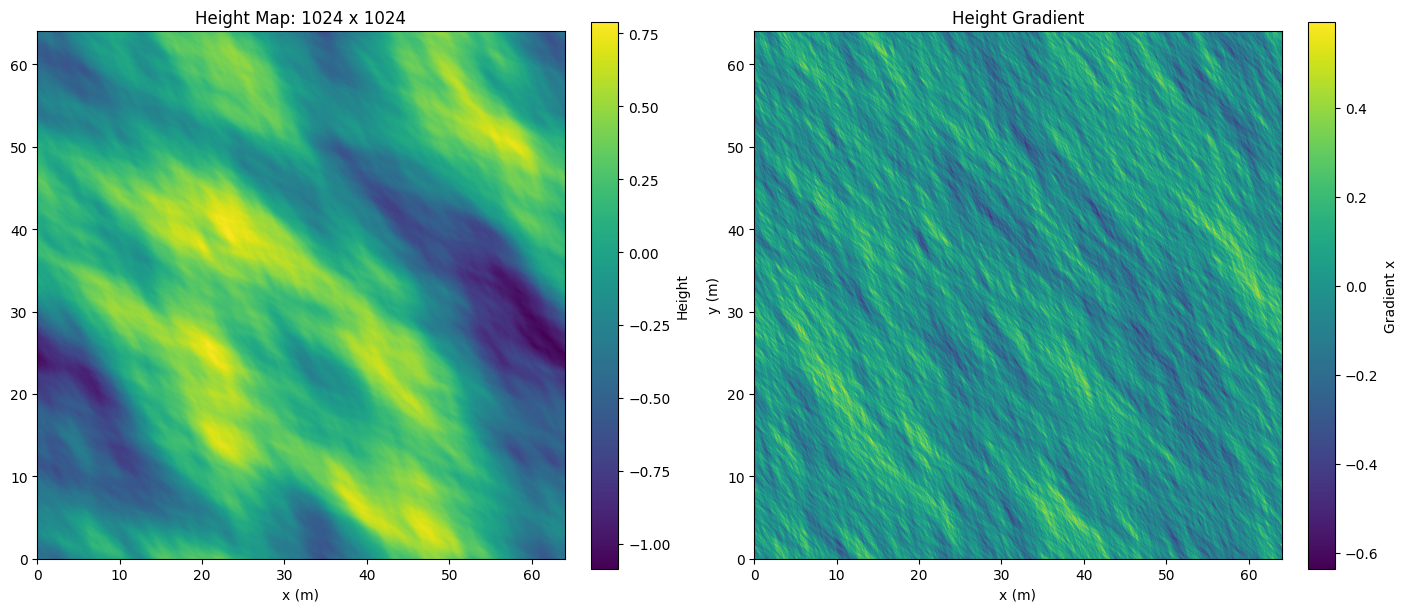
Reflection, Refraction, Absorption, and Scattering

The ocean is a complex medium that can reflect, refract, absorb, and scatter light. The Fresnel equations describe how light is reflected and refracted at the ocean surface. Reflection is given by

\[\hat{n}_r = \hat{n}_i - 2(\hat{n}_i \cdot \hat{n})\hat{n}\]

where \(\hat{n}_r\) is the reflected normal, \(\hat{n}_i\) is the incident normal, and \(\hat{n}\) is the surface normal.

Transmission is governed by refraction of light through water, which is given by

\[\hat{n}_t = \frac{\eta_1}{\eta_2}\hat{n}_i - \left(\frac{\eta_1}{\eta_2}\hat{n}_i \cdot \hat{n} + \sqrt{1 - \left(\frac{\eta_1}{\eta_2}\right)^2(1 - (\hat{n}_i \cdot \hat{n})^2)}\right)\hat{n}\]

where \(\eta_1\) is the refractive index of air and \(\eta_2\) is the refractive index of water. The refractive index of air is defined to be 1 and water around 1.33. Note, there is a case where total internal reflection occurs, which is when the angle of incidence is greater than the critical angle. In this case, the light is reflected back into the water. The critical angle is given by

\[\theta_c = \arcsin\left(\frac{\eta_2}{\eta_1}\right)\]

The Fresnel equation determine the transmission, \(T\) and reflection \(R\) coefficients, which are multipled by the incident light for each scenario. As given in [1]

\[R = \frac{1}{2}\left( \frac{\sin^2(\theta_t - \theta_i)}{\sin^2(\theta_t + \theta_i)} + \frac{\tan^2(\theta_t - \theta_i)}{\tan^2(\theta_t + \theta_i)} \right)\]

where \(\theta_i\) is the angle of incidence and \(\theta_t\) is the angle of transmission. The transmission coefficient is given by

\[T = 1 - R\]

by conservation of energy.

Since water is a absorbing as well as scattering medium, we can approximately model the attenuation of light by Koschmieder [2]

\[L = L_0 e^{-\beta d} + \alpha (1 - e^{-\beta d})\]

where \(L\) is the resulting luminance, \(L_0\) luminance of directional light, \(\beta\) scattering coefficent, \(d\) is the distance between the ocean surface intersection point and the ocean floor.

Furthermore, to model the fact that absorption of different colors of light depends on depth, we linearly interpolate between a uniform albedo and deep water albedo between depths 0 and \(d\) (m) and beyond \(d\) we use the deep water albedo.

Two Stage Light Transport

We describe a two stage light transport model for ocean imaging. The first stage is the light transport from the light source (directional light from the sun) to illuminate the ocean bottom surface. The second stage is the light transport from the ocean surface to the camera.

In the first stage, we compute a lightmap of the ocean floor, where each pixel \((x, z)\) corresponds to the color of the ocean floor at \((x, z)\). We begin by tracing directional light to the wave, refracting it, and then tracing it to the respective point on the ocean floor where it is accumulated, producing a radiance map. Tracing an be vectorized by solving for the positions on the ocean bottom where the ray ends. To account for attenuation, we also need the distance the ray has traveled. Assuming constant depth for now, both can be handled via ray-plane intersection. We will discuss the more complicated varying depth case in the next subsection.

The above method can produce realistic caustic effects. Some points may not recieve light due to the limited resolution of the grid, however, we can take an max pool to smooth out the radiance map. The ocean bottom texture map is multipled by the radiance map to get the lightmap.

The next stage, we can trace rays from the camera to the ocean surface, refract them (refraction is symmetrical wrt to time-reversal), and then trace them to the ocean floor. The corresponding lightmap value is traced and attenuated again back to the surface and accumulated at the corresponding pixel.

Below we show from left to right the original image, bottom lightmap, and final aerial image generated from the process for the wavemap shown before assuming constant depth of the ocean surface. Notice the caustic effects in the lightmap and final image, which we term the corrupted image since our ultimate goal is to see through the ocean.

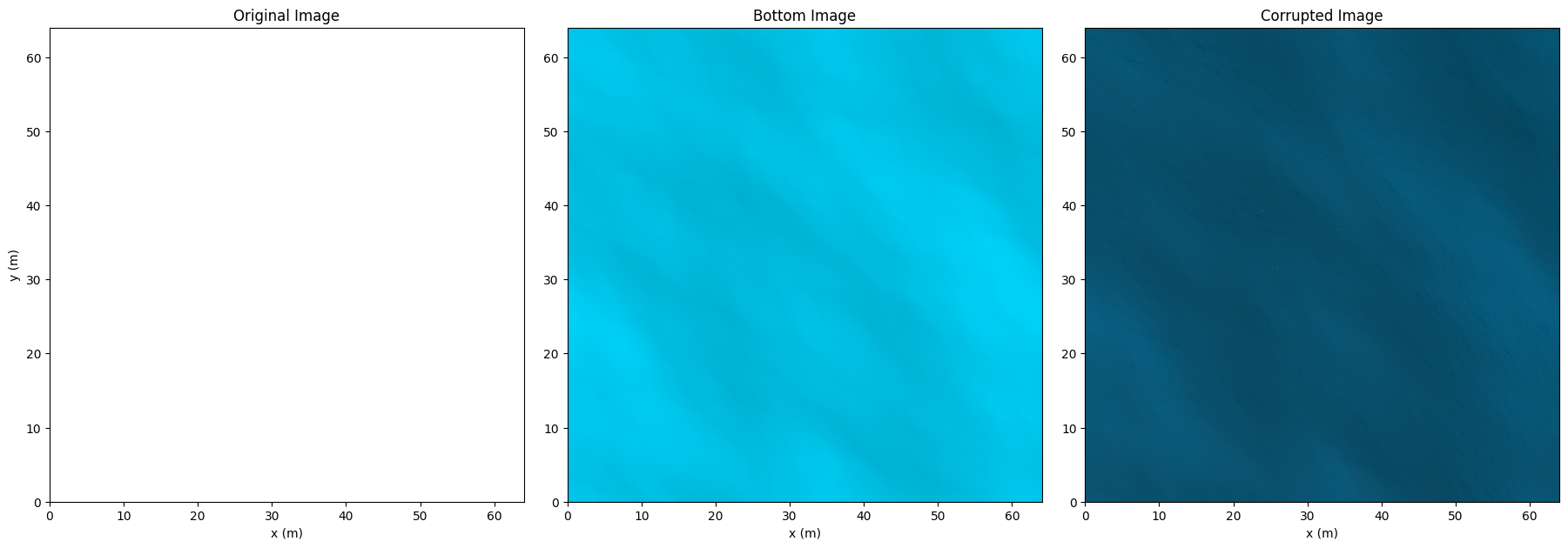
Nonconstant Depth

The constant depth case takes \(O(1)\) time and \(O(HW)\) memory on a parallel computation model e.g. GPU when performing vectorized ray-plane intersection. Dealing with nonconstant depth is tricky because the ray might terminate before it hits the plane defined by the min depth. We showcase an implementation that \(O(1)\) time and \(O(HW\text{nsteps})\) memory where \(\text{nsteps}\) is defined as the maximal number of steps a ray will take at a resolution until it terminates. The idea is we discretize the ray’s path into nsteps and check for intersections at each step by seeing if the position of the ray is above the depth. The resolution is determined as

\[\delta = \min(dx, dz) = \min(L_x/N, L_z/M)\]

since any ray must travel at least \(\delta\) distance to cross a cube of dimensions \(dx \times dz \times \epsilon\) for any \(\epsilon\). We can upper bound \(\text{nsteps}\) with \(d_{\min} / \delta\) where \(d_{\min}\) denotes the distance to the plane defined by the min depth.

However, this process may result in excessive memory usage. We can convert memory into time by accumulating over depth range batches resulting in \(O(B)\) time and \(O(HW\text{nsteps}/B)\) memory. \(B = 2\) is sufficient for up to \(25\)m depth.

Below we show a few examples of nonconstant depth.

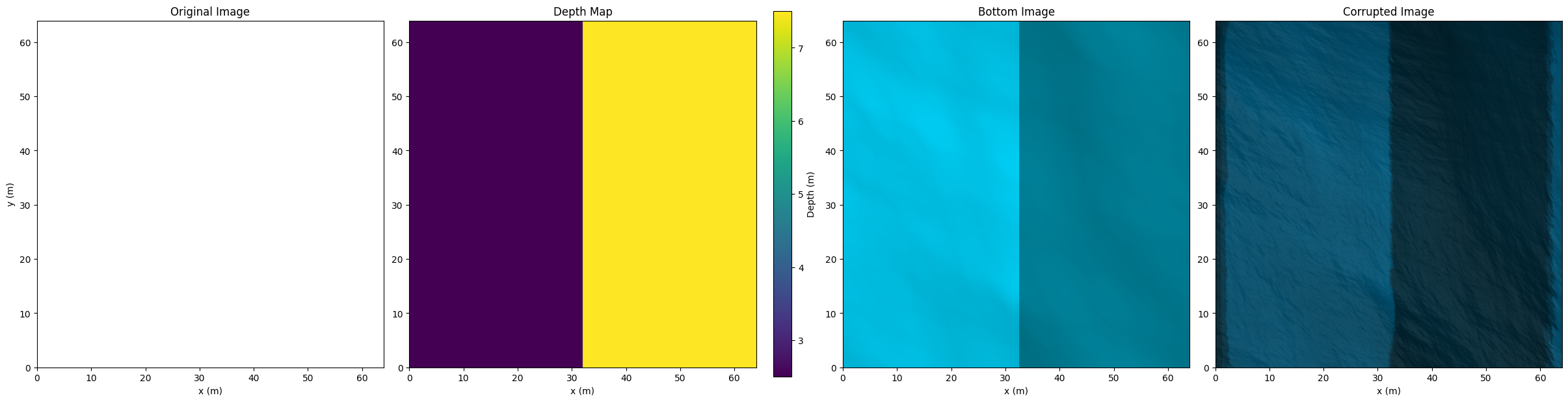
In the above example, we observe artifacts at the end due to assuming repeatedly tiled ocean bottom for depth and texture as well as wave patch.

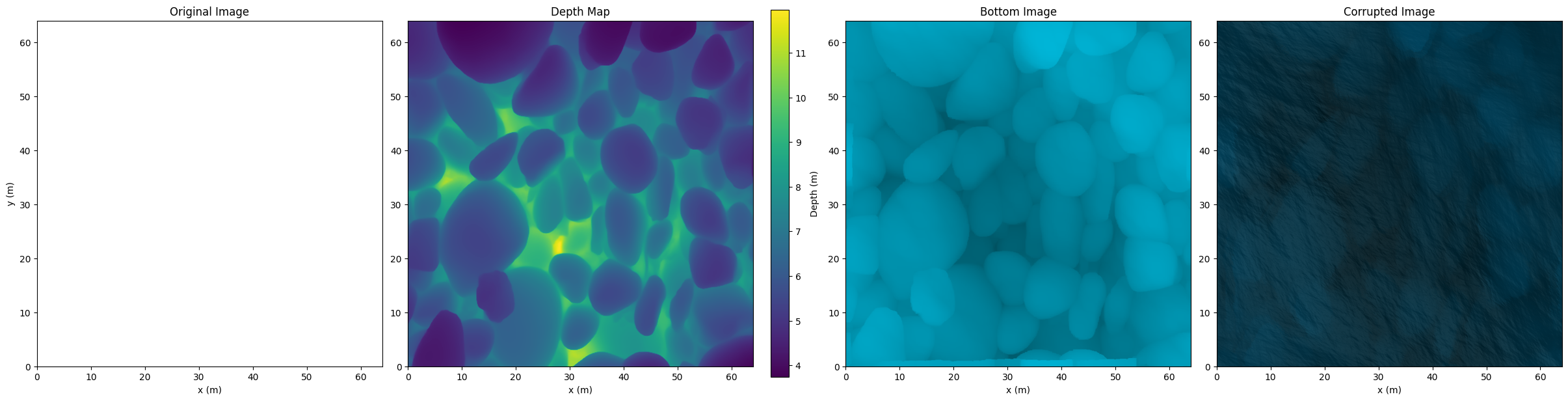
Secondary Reflections

Reflection in the ocean is very complex as not only do we need to consider direct reflection of directional light, but also secondary reflection from waves. We model reflection as a power function

\[R \cdot I \cdot \alpha(\hat{n}_r \cdot \hat{r})^\beta\]

where \(R\) denotes the reflection coefficient, \(I\) light intensity, and \(\hat{r}\) the camera ray. \(\alpha, \beta\) can be tuned and define the power function. Intuitively, higher \(\beta\) sharpens the reflection i.e. less water exhibits specular properties.

Putting everything together we are able to obtain some examples under different parameter settings (zoom in to see the details)

Direct sunlight from above

Inclined sunlight direction

We can decrease the patch size and increase the wave dampening to get cool distortion effects.

Thank you for reading! This post will be updated soon with a solution to the inverse graphics problem of removing the ocean effects from the image.

References

[1] Tessendorf J., Simulating Ocean Water, 2004
[2] Koschmieder, H., Theorie der horizontalen Sichtweite. Beitr. Phys. Atmos. 12, 33-58, 1906